Color segmentation

In most of images that we take during data acquisition, we only want part of the image that contains that data the we need. There are a lot of ways to do this; it can even be done using template matching. For this activity, what we do is we use the color of the region of interest (ROI) to separate it from the whole image.

There are two techniques that can be done in color segmentation. They are the Parametric and Non-Parametric segmentation. Both of these techniques use a portion of the ROI.

Each pixel in a colored image has RGB values. What we do in parametric segmentation is that we take the fraction of the RGB values that is in each pixel in the portion of the ROI. That is:

where , and . However, we can see that b can be seen as a function of r and g, given by:

This means that we only need to obtain the r and g values.

In parametric segmentation, we obtain the r- and g-values of a portion of the ROI. Then we obtain the mean r and mean g values, given by μ_r, μ_g and the standard deviation values, σ_r, σ_g, respectively. After obtain the mean and standard deviation, we obtain the probability that a pixel belongs to the ROI using the r and g values of the pixel. The probability for r (and g) is given by:

where r is the r-value of the pixel. The same form is also used for g-values. After obtaining p(r) and p(g), we obtain p(r) * p(g) which will give us the probability of the pixel being part of the ROI. We show in figure 1 the image that we used, and in figure 2, the portion of the ROI where the mean and the standard deviation are obtained.

Figure 1. The ROI are the flowers.

Figure 2. A portion of the flowers.

Figure 3 shows the probability of each pixel. We can see that the flowers are separated from the whole image.

Figure 3. The flowers are separated from the other parts of the image.

For the next technique, we use a histogram. This histogram is created using the r and g values of the portion of the ROI. We convert the r and g values into integers and binning the image values in a matrix (Soriano, 2013). The quality of the segmentation depends on the size of the bin that is used. In figure 4, we show the result of the non-parametric segmentation with different bin sizes.

Figure 4. left to right, top to bottom: bin size = 2, 4, 8, 16, 32, 64, 128, 256

From figure 4, it can be seen that the lower the bin size, the constraint becomes too loose such that even other objects in the image are segmented. The higher the bin size, the lesser the details are segmented until such that even some of the objects that are needed are not segmented. It all boils down to choosing a good bin size.

In comparison, the parametric segmentation yields better results, since the flowers have a higher brightness, and no other objects are captured. However non-parametric segmentation is faster since the look up table (the histogram) is present and no further calculation is needed. I show another example in figure 5.

Figure 5. The left image is the original, center the result of parametric segmentation, and right the result of non-parametric segmentation. The difference between the quality of parametric and non-parametric segmentation is seen. The parametric segmentation captures more area of the flowers.

I give myself a grade of 6/10, since this blog is overdue. I thank Ms. Abby Jayin for her help in understanding the concepts.

Sources:

Color Segmentation by Dr. Maricor Soriano.

Image Compression (PCA)

In the old age where a diskette (ha! hipsters can relate) is equivalent to today’s USB in terms of usefulness, Storage was once a problem, and in finding a way to solve this, they have come across what is currently known as image compression, which is still being used today (hello JPEG). In this activity, we show how to compress images using Principal Components Analysis (PCA).

Basically what PCA does is that it converts a set of correlated signals into orthogonal functions whose sums (with their respective coefficients)  can reconstruct any of the signals. (I do not want to indulge in here. :PPP) If we have a set of functions, f1, f2, f3, …. , fn,  then we can obtain a set of orthogonal functions W1, W2, W3… Wm such that:

Where is the coefficient for the function . The functions are called the principal components. However, each has a different percent contribution to the reconstruction of the image. In Scilab, and can be obtained using a single line of code. . If X is the matrix containing the signals (each column being an individual signal), the principal components and the coefficients can be obtained by:

where facpr is the matrix containing the principal components and comprinc the matrix containing the coefficients. Lambda gives the percent contribution of each principal components to the signals.

In image compression, what we do is that we cut our image into parts. Then we convert each part to a single matrix with size . Each  matrix will be one signal. Then we concatenate all the signals into one matrix which will be input to the pca. For this activity, we use .

There will be principal components. What we will then do is try to reconstruct the images using the principal components. Because each principal component have different percent contribution, we will investigate what will happen to the reconstruction if we use only n principal components (0<n<100).

We use a picture of a cat (well its a tiger but…. still a cat).

A cat.

In the figure below, we show the difference of the original picture (in grayscale) to the reconstruction images.

The topleft figure is the grayscale image of the cat. The top center is for n=1, top right is for n = 5, bottom left is n = 10, bottom center is n = 50 and bottom right is n = 100.

From the figure above, we can see that the higher the number of principal components used, the better the quality. However, it can be observed that for n = 50 and  n = 100, the images do not vary much. This is due to the percent contribution of the principal components.

In the next figure, we show what the principal components look like.

The principal components are each 10 x 10 part of this picture.

We show another example. This one came from the anime Fate zero, where the protagonist is a female swordsman…..well you can search it if you like.

The number of principal components are the same as the cat figure.

The author gives himself a score of 9/10 for this work. He acknowledges Mr. Tingzon for the help. 🙂

Sources:

Wikipedia

Dr. Maricor Soriano

Image and Music (activity 12)

In this activity, we play notes on a score sheet using image processing and scilab (I know, tones from programming languages are usually pure tone, they do not emulate real world instruments. Anyway, still its cool). The score sheet that I used is a score sheet of a common song, “Twinkle Twinkle Little Star”.

Figure 1. Score sheet from mamalisa.com. One of the coolest tones ever!

We read the image of the score sheet in scilab and do the usual (imread, rgb2gray, etc). The next thing that we do is crop a part of the image shown in figure 2.

Figure 2. In case you’re wondering what this is, this is the oval in the end of a half note.

What we are trying to do here is that we want to obtain the coordinates of the notes, at least one coordinate of each note whose qualification is consistent. This is because the row of the coordinate will be used to obtain the tone and the column used for the duration and sequence of the notes.

So what we are going to do next is to edit figure 1 such that the notes are sequential. To drive this idea home, I show figure 3.

Figure 3. The notes are now sequential. This is to facilitate better sequencing of notes.

We then do template matching of figure 2 and figure 3. After thresholding, we obtain the relative position of the notes. This works because all the notes are quarter and half notes so figure 2 is found in all the notes that are present.

Figure 4. The white dots are the position in which the template matching has the highest values.

We obtain the position of the white dots in figure 4, the x being the tone and y being the sequence and the length of each note. From figure 1, the notes are in the key of C. Therefore Do is C, Re is D, Mi is E, etc. Using the table from http://www.phy.mtu.edu/~suits/notefreqs.html, we can convert the x-axis into sinusoids. Using the sound function, we can play the notes. I currently cannot upload the file.

The author gives himself a grade of 9/10 for this activity.

Image Enhancement (Frequency)

We try to enhance images in the Frequency Domain (hello again, FFT. Haha). For some background, it is recommended to read on the Fourier transform first. 🙂

Anyways, Image enhancement is almost always done in the frequency domain. This is because noise and spurious parts of the image cannot be removed from the image itself. However, these unwanted distortions can be removed in the frequency domain since they have different (higher) frequencies than the important details of the image. What generally happens is we multiply a mask in the frequency domain to remove the higher frequencies. But if we multiply in the frequency domain, we are actually performing a convolution in the image domain. So before everything else, lets discuss convolution! (For a little bit of background, you may want to read on my previous post. Or search it on google. Or read arfken. Whichever.)

Convolution is actually smearing of two functions to create another function that has the properties the two functions. This is in contrast to correlation, where the resulting function is the similarity of the two functions. In more simplified words, convolution is a union of properties, while correlation is an intersection of properties. A convolution is presented below:

or:

The integral is quite cumbersome to work with, especially when coding. There are some programming languages that have a convolution function, but generally the integral itself has to be worked out. Thankfully, performing the Fourier transform simplifies things:

where the is the Fourier transform operator. I have already performed some convolution myself. Figure 1. shows a the result of convolving circles of different sizes and their Fourier transforms.

Figure 1. The left side shows the result of the convolution in the image domain. Convolving with a sum of Dirac delta functions is just placing the center of the image in that position. In the frequency domain, the convolution is just the multiplication of the Fourier transform of each function.

The Fourier transform of a two-Dirac delta function which is symmetric wrt the y-axis is a sinusoid while the Fourier transform of a circle is an Airy pattern. The airy pattern is very prominent in the right side, though the sinusoid is not that discernible. This could be due to the fact that the Dirac deltas are far from the center, hence they are high frequency. High frequency in images are the ones that cannot be discerned if the image is rescaled to a smaller size.

We show some more convolution. This time the same Dirac delta function and a square (figure 2), and a Gaussian (figure 3).

Figure 2. Convolution of a square and the Dirac delta function.

Figure 3. Convolving a gaussian with the same Dirac delta function.

The above images show the end result when the convolution is done in one plane; multiplication is done on the other. However, I haven’t really shown you what really happens when you convolve two things in the same plane. Figure 4 show what happens when you convolve two functions.

We generate Dirac deltas in random places and convolve them with the following patterns (Im sorry, i wasn’t able to convolve them with the same set of Dirac deltas. Since the position are random, the Dirac deltas are not the same. :[..)

Figure 4. n is the number of Dirac deltas. A comparison shows that for the x pattern, we can observe ghost spectra.

Figure 4 shows the convolution between Dirac deltas and square function, and Dirac deltas and the x pattern. The square and the x pattern is simply place where the Dirac delta is placed.

Figure 5 shows the Fourier transform of uniformly distributed Dirac deltas in the x and y axis, with different distances from each other.

Figure 5. The FFT of Dirac deltas in the x and y-direction with different distances from each other (1, 2, 4, and 8).

Image enhancement

Now we finally get to enhance some image! First off, we’ll try to enhance the famous image, the image from the lunar orbiter, shown in figure 6.

Figure 6. The image from the lunar orbiter.

As observed, there are a lot of spurious white lines in the image. This is because the image was transmitted part by part so there was some irregularity. We try to remove the whitelines by multiplying a mask in the Fourier domain. Applying FFT:

Figure 7. The image is in log scale since the low frequency details have higher magnitude such that all the other details seem black.

We can see a lot of white noise, though their magnitude is smaller. If we refer to figure 5, we can estimate the frequency of the inconspicuously white lines, and in figure 7, that would be the straightlines. We multiply a mask, an example of which is shown in the next figure.

Figure 8. The mask that was used.

Observing figure 8, we may point out that the center is being left out. This is because, in many images, the important details often have low spatial frequency (of course this applies to most signals as well), so we have to retain those information. We multiply figure 8 and 7 then apply IFFT. The result is shown in figure 9.

Figure 9. The output of applying a mask in the Fourier domain.

In figure 9, the white lines become lesser. However, they can still be seen. It is recommended to thicken the lines in figure 8 to remove more. However, this has the probability of removing some important detail, so we did not do it here.

In figure 10, we show another example of an enhanced image, a painting by Dr. Vincent Daria, Fredericksborg.

Figure 10. The Fredericksborg.

The top left image is the painting before doing anything (converted to grayscale). The lower left is the FFT then the lower right is the mask. After applying the mask to the FFT of the image and applying IFFT, the top right image is obtained. It is obviously cleaner than the one on the right. The brush strokes are removed.

The author gives himself 10/10 for completing the minimum requirements.

acknowledgements to Abby for helping.

Fourier transform

We finally get to play around with Fourier transform!

For this activity, we are going to familiarize ourselves with the discrete Fourier transform, specifically the Fast Fourier Transform (FFT) by Cooley and Tukey. Then using the FFT, we apply Convolution between two images. Next is Correlation, where we use the conjugate of the image. Lastly, using convolution, we do an edge detection.

1. Familiarization with FFT.

One theorem in mathematics is that, all wave forms can be decomposed into sinusoids. That is, the function can be expressed as a sum of sines and cosines. Though this theorem may sound gibberish at first, we will explore the wonders that this theorem has given us. 🙂

Breaking down a function into sinusoids gives us the “ingredients” in making that function in the frequency domain. This is done using the Fourier Transform, the equation as follows:

where 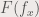is the FT of the function 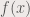. 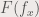is the amplitude of the frequencies found in 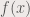. The equation above is for one dimensional Fourier transform, where graphing 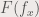will give the peaks corresponding to the values of (frequency) that the function 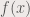contains. However, here, we are going to deal with two-dimensional Fourier transforms since we are dealing with images. The 2D Fourier transform is shown:

where 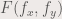is the 2DFT of 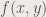, being the frequencies in the x direction and the frequencies in the y direction. However, in the real world, data is discrete when existing sensors, or sampling instruments, sample any data set. Meaning that data is not continuous and that only some values of the data set is captured. An example of this would be the camera. When we look at the properties of the image captured by the camera, we see something that is called the pixel. Images are composed of pixels, so when an image is zoomed in, the details become distinct and not continuous; squares of different colors can be observed. When you compare this to the real world, you cannot see small squares when “zooming in” the real world objects. Though you cannot determine position and momentum of particles in exact values at the same time, but that topic will not be tackled here. =,=

Because real data is discrete, we cannot apply the integral above, since integrals are applicable to continuous systems. Cooley and Tukey (1965) derived the fastest discrete Fourier transform algorithm still used by many programming languages today. The algorithm is often called the Fast Fourier transform (FFT). It is shown by the following equation:

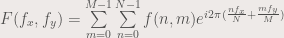
where f(n,m) is the value of the image in the 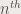x value and 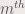y value with size . This algorithm is being used in a lot of applications; radar, ultrasound, basically almost anything that includes image processing.

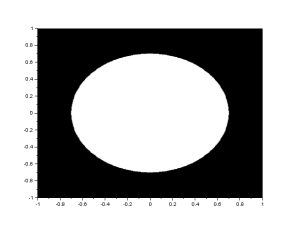
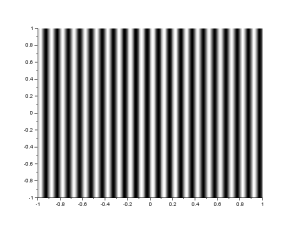
The FFT algorithm in most programming languages has the diagonals of the output interchanged. Because of this, a function called the fftshift is often used to correct the placement of the diagonals. In figure 1, I show the result of the FFT of a circle with aperture radius equal to 0.1 of the maximum radius that can be created, with and without the fftshift function:

Figure 1. We show the FFT of a circle(left) without(center) and with(right) the fftshift. Analytically, the FFT of a circle is an airy pattern, which can be seen in the image on the right.

We can see that the fftshift function is really important to obtain the correct FFT of an image. Figure 2 shows the FFT of the letter A, and also the images showing what happens if FFT is applied twice to the same image and if IFFT is applied after the first FFT.

Figure 2. The top left image shows the letter A. The top right image shows the FFT of letter A (already fftshift-ed). The bottom left image shows what happens if you apply FFT twice to the letter A. The bottom right shows if you apply the inverse FFT after application of FFT to letter A.

It can be seen in figure 2 that if FFT is applied twice, the image becomes inverted, while if IFFT or inverse FFT is applied after application of FFT, the image becomes upright. The next image shows the FFT of circles with different sizes, ranging from 0.1 of the maximum radius to 1 times the maximum radius.

Figure 3. The circles with different radii, shown with their FFTs. The circles have width equal to (from left to right) 0.1, 0.2, 0.4, 0.6, 0.8 and 1 times the maximum radius. The results agree with the theoretical that says, the smaller the circle, the more detailed the airy pattern is. The theory will not be discussed here.

2. Convolution

Convolution is a linear operation that basically means smearing one function with the other (Soriano, 2013) such that the resulting function has properties of both functions. The convolution is represented by an *. So if two functions are convolved with each other, they are represented as (in integral form):

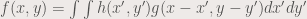
or in short hand form:

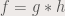
Since the FFT is a linear transform, and convolution is a linear operation, the FFT of a convolution is multiplication of the two functions being convolved. Basically:

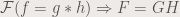
where F, H and G are FFTs of f, h and g, respectively. Convolution is used to model sensors and instruments that are used to sample data sets, since sensors also affects the values of the data, whether the sensor be a linear system or second order system or higher order. An example of a sensor that affects how data is captured is a camera, where the resulting image (f) is a convolution of the data itself (g) and the aperture of the camera (h).

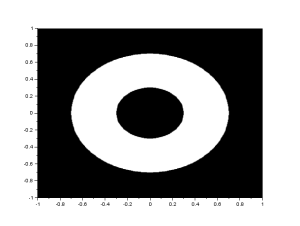
The equation of a convolution is oftentimes more difficult than just applying FFTs. So in this part of the activity, we apply FFT to both functions g and h, and multiply them, then apply IFFT to obtain the convolved function f. With g as the VIP image and h as the camera aperture, we apply convolution operation. We show the results in figure 4.

Figure 4. The top left figure is the VIP target. Then the following images (from left to right, top to bottom) are the results from the VIP image being convolved with different aperture sizes (1.0, 0.8, 0.4, 0.2, 0.1, 0.05, 0.02)

It can be observed from figure 4 that the smaller the aperture size, the clearer the image becomes. This is because the smearing becomes less and less as the aperture size becomes smaller. So the smaller the aperture size, the higher the image quality.

3. Correlation

The second concept that we will discuss here is called correlation. Correlation is the link between two data sets, or in this case, between two images. This concept is often used in template matching because it answers the question “how same are these two images?”. The equation of correlation is given by:

or in shorthand notation:

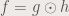
We can see that the integral equation of correlation looks like the convolution. The two are related by the following, where we can show correlation in a convolution equation:

The same as convolution, correlation is a linear operator, so applying FFT will lessen our load (such as not doing the integral shown above). The correlation has the following property:

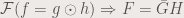
where is the complex conjugate of . We use the correlation in template matching, or in finding out how similar are the two images in a position . We use the sentence THE RAIN IN SPAIN STAYS MAINLY IN THE PLAIN and correlate it with an image of the letter A using the FFT relationship above. Then by thresh holding, we obtain the positions in which the images have a high correlation. We show the result in figure 5.

Figure 5. We do template matching using the sentence THE RAIN IN SPAIN STAYS MAINLY IN THE PLAIN and the letter A. This basically means we find the places in the second image where the first image can be found, or is most similar. The white dots in the third image in the right shows those locations. If we observe further, the white dots in the third image corresponds to the locations of the A’s in the second image. Because these are the places where the letter A is most similar in image 2.

We can see that after thresh holding, the places with the highest correlation value are the places in the second image where the letter A is found. This is what template matching means.

4. Edge Detection

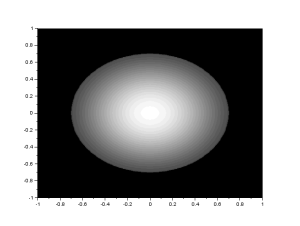
Edge detection is basically convolving an image with an edge pattern. Patterns that add up to zero, often small patterns, are called edge pattern. In this exercise, the edge patterns are just 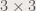matrices that are padded with zeroes to reach the size of the image being convolved with. We show an example below and its Fourier transform, to show why it is an edge pattern.

Figure 6. The edge pattern on the left, and its FFT. Multiplying this FFT to the FFT of any image and applying IFFT to it will give us the edge of the image. This is because the edges of the objects in any image can be seen as the high frequency parts of the image.

There are many different edge patterns. The edge pattern in figure 6 has the following matrix:

-1 -1 -1

-1 8 -1

-1 -1 -1

We call this the spot pattern. We also have the horizontal, the vertical, the diagonal, all shown below

-1 -1 -1                            -1 2 -1                                    2 -1 -1

 2  2  2                             -1 2 -1                                   -1 2 -1

-1 -1 -1                            -1 2 -1                                   -1 -1 2

We can also manipulate the spot pattern such that the number 8 is off-center. We can have the following matrices

8 -1 -1         -1 8 -1       -1 -1 8          -1 -1 -1             -1 -1 -1

-1 -1 -1       -1 -1 -1      -1 -1 -1         8  -1 -1              -1 -1  8

-1 -1 -1       -1 -1 -1      -1 -1 -1         -1 -1 -1              -1 -1 -1

and the following:

                 -1 -1 -1          -1 -1 -1            -1 -1 -1

                 -1 -1 -1          -1 -1 -1            -1 -1 -1

                  8 -1 -1          -1  8  -1            -1 -1  8

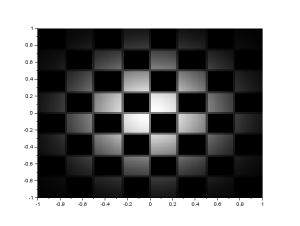
If the number 8 is off-center, we call the matrix depending on the position of the 8. So the above matrices are called, from left to right, top to bottom: northwest, north, northeast, west, east, south west, south, and southeast. Using the above matrices as edge patterns, we apply convolution with edge pattern and the VIP image. For the horizontal, vertical and the diagonal edge patterns, the results are shown in figure 7.

Figure 7. Edge detection with horizontal, vertical and diagonal edge patterns (from left to right).

We can see in figure 7 that the edge that is most prominent is the edge that follows the edge pattern. For the horizontal edge pattern, the horizontal edges are the most prominent. Likewise for the vertical and the diagonal edge patterns. Figure 8 shows the edge detection using the 9 different spot edge patterns.

Figure 8. Edge detection using spot edge pattern. The left images show the result after using edge spot patterns for edge detection. The placement of the image correspond to the placement of the number 8 in the 3 x 3 matrix used. The right image shows the FFT of the spot edge patterns, with the placement of the image, again, corresponds to the placement of the number 8 in the 3 x 3 matrix.

From figure 8, we can see the the southwest and the northeast edge patterns are the same. The same goes for the northwest and the southeast; the north and the south; and the east and the west. These edges can be used for determining the area of the image by using the Greens theorem. Images can have different prominent lines, so the optimal edge pattern is different for each image.

I have shown the tip of the iceberg of the uses of the FFT. There are a lot of uses of FFT in many different fields, particularly in sensing and signal processing.

The author gives himself a grade of 10/10 for completing the minimum requirements needed for this activity.

Acknowledgements go to these sites:

http://fourier.eng.hmc.edu/e180/e101.1/e101/lectures/Image_Processing/node6.html
https://en.wikipedia.org/wiki/Fourier_transform
http://www.mathsisfun.com/data/correlation.html
http://en.wikibooks.org/wiki/Signals_and_Systems/Time_Domain_Analysis

I will not place here the codes that I have used.

Image enhancement

We were tasked to enhance an image by changing the cummulative distribution function (CDF) of an image. The CDF of a graylevel is just the sum of all the number of pixels with the grayvalue, from grayvalue of  0 to some grayvalue K. This is normalized by the number of pixels present in the image. The CDF is obtained by obtaining the histogram of the grayscale of an image. The histogram is then normalized to obtain the probability density function of the image (PDF). Obtaining the cummulative sum will give us the CDF. The figure we enhance in this activity is shown in figure 1, along with the CDF of the image.

Figure 1. The image to be enhanced is on the left and the Cummulative Distribution Function is on the right. The CDF shows a sudden increase in the amount of pixels having low gray levels. This means that the picture is mostly black.

LINEAR

First, to enhance the image in Figure 1, we impose a linear CDF, that is, a normal PDF. This is quite easy to do since the goal is a linear CDF, we just need to multiply the CDF of the original image by 255. The general process is shown in figure 2.

Figure 2. The steps on how to alter the gray scale distribution. (1) The gray level of the pixel must be known, and the corresponding value in the CDF. Then the CDF value is projected onto the desired CDF, and finally, the corresponding gray level of the pixel is the new gray level.[1]

For the first part, we obtain the enhanced image with a linear desired CDF. Figure 3 shows the enhanced image, along with the CDF of the resultant image, and the desired CDF.

f igure 3. The enhanced image with the resulting CDF(center) and the desired(right) CDF. It can be seen that though the resulting CDf kinda follows the desired CDF, the resulting CDF shows a ladder pattern

From figure 3, it can be seen that the resulting CDF follows the desired CDF but has a ladder pattern. This means that even though we force the CDF to change, the previous CDF of the image still acts as a constraint, preventing the resulting CDF to completely follow the desired CDF.

SIGMOID

A sigmoid function is a function that looks like the letter S. The function is given by:

                                                                                                             S(t) = 1/(exp(-t) + 1)                                                                     (1)

If we add the scaling factors, the translation and the size of the sigmoid function can be changed. Applying the scaling factors, (1) becomes:

                                                                                                          S(t) = 1/(exp((-t + T)/d) + 1)                                                          (2)

Where T is the translation and d is the width of the sigmoid. Conversely, we can find the t if we are given the S(t). In our case, the S(t) is the desired CDF and t is the gray level corresponding to the CDF. Doing some mathematical derivation, we arrive at:

                                                                                                                 t = -dlog(1/s – 1)  +T                                                                     (3)

First we need to find the optimum T. Our code (see below), has a line with a function uint8. this ensures that the values are between 0 and 255. This function obtains the modulo of every value of 256. Choosing a random d to find the optimum T, (d = 32), we generate the following images, with different T.

Figure 4. Images showing different translation T in the computation. On the upper left is T = 0, and with 30 increments thereafter. We know that the image was created with a black pen on a white background. In the figure above, the image we picked is the image in the lower leftmost figure. this is because, the contrast is not that high or low.

From figure 4, we used T = 150. For the next part, we change the width factor d in the calculation, from 1, 2, 4, 8, 16, 32, 64, and 128. Figure 5 shows the CDF from 1 – 128 (in exponents of 2). (I call it width since it seems to be similar to the gaussian standard dev where beam width is 1/e)

Figure 5. The CDF used, with different CDF sizes ( innermost is 1 while outermost is 128, in exponents of 2)

Using the CDFs above as the desired images, we generate the following images(with the corresponding resulting CDF’s):

Figure 6. The enhanced images with different CDF widths. Left column has width = 1, 2, 4, 8(top to bottom), While the right column has width = 16, 32, 64, 128 (top to bottom)

What seems peculiar in figure 6 is that, when the CDF width is chosen to be 128, there can be no discernible letter in the image. Looking at the image, we could say that the most enhanced image would be the image with width equal to 32 and translation equal to 150. it can be seen that the resulting CDF follows the desired CDF exept for the lower 3 images in the right column.

Other softwares also have this kind of manipulation. The histogram can be manipulated by dragging the diagonal line. however I am not going to discuss that here.

I give myself a credit of 11/10 since i investigated the effect of translating and manipulating the width of the sigmoid.

[1] Laboratory manual by Dr. Maricor Soriano

CODE for Sigmoidim = imread(‘C:\Users\ledy_rheill\Google Drive\Documents\Academics\13-14_1stsem\AP186\activity 6 27 Jun 2013\image.png’);

im_gray = rgb2gray(im);//convert to grayscale

his_plot = CreateHistogram(im_gray, 256); // obtain histogram

size_xy = size(im_gray);//obtain sizes for normalizatio

narea = size_xy(1,2) * size_xy(1,1); //take area for normalization

summed_his = cumsum(his_plot)/area; //normalized cummulative sum

//first we use a linear cummulative distribution function where the probability distribution function is normal (cdf is a line), therefore we just multiply the cdf of the original image by 256

new_summed = summed_his(im_gray + 1);//converts the image gray values to the corresponding cummulative sum. there are 256 values of cdf, but array starts at 1

im_gray2 =-1*log(2 ./(new_summed + 1.000002) – 1) ;// since CDF is linear, the correspondence is also linear, so we just multiply the CDF by the value of the pixel with cdf equal to 1, which is

max(new_summed) * 256 -1im_gray_new2 = matrix(real(im_gray2), size_xy(1,1), size_xy(1,2));// since it was flattened to one d, we convert it back to 3D

im2 = uint8(im_gray_new2);//convert to 8bit imageimshow(im2);

his_plot2 = CreateHistogram(im2);summed_his2 = cumsum(his_plot2)/area

imwrite(im2, ‘C:\Users\ledy_rheill\Google Drive\Documents\Academics\13-14_1stsem\AP186\activity 6 27 Jun 2013\sigmoid_cdf_128width_flower.png’)

Greens area

For this activity, we were tasked to obtain the area of shapes using greens theorem. using the edge function of scilab, we are to obtain the area and by analytically solving for the area, we are to compare the results from the greens theorem to the analytically solved area.

first, I obtained the area of 10 circles. The result of the edge function is also shown. (I only show one circle).

Figure: the circle on top, the result of the edge function on the bottom.

After obtaining the edge, I obtain the area using the discretized green’s function. I repeat the process for 10 different circles to obtain the average deviation from the answer using the equation for the area. I obtained a deviation of 0.62%.

I also did the same thing for rectangles.

Figure: Edge detection of a rectangle

After doing the same process for rectangles, I obtain a deviation of 0.46%.

We are also tasked to obtain the area of any location of interest using the greens theorem. I chose to find the area of the Quezon Memorial Circle, which has an area of 27 hectares, or 270,000 square meters. After isolating the Quezon Memorial Center and obtaining the edge, I have the following images:

After applying the Green’s theorem, i obtained an area of 233935.44 square pixels. Using the scale bar, 90 pixels is 100 meters, therefore 8100 square pixels is 10000 square meters. using ration and proportion, the area of the memorial center is 288809.1853 sq. m. or 28.88 hectares. This value is 7.0% from the theoretical value.

I obtained the area of the Quezon memorial center from:

http://www.1stphilippines.com/pc-30f6af23af986d2e822e18015fd22ce1.html

The author gives himself a grade of 9/10 since he was only able to do the rectangle and the circle.

Tinkering with images :)

For this activity, we were told to tinker with images and their properties. first stop was to know properties of images downloaded from the web. And since i like flowers, let me show you some of them 🙂 (i’ll only show the camera or the software used)

Canon PowerShot S45,  1693 x 1413 pixels, 24-bit 180dpi resolution (vertical and horizontal)

F-stop : f/2.8, exposure: 1/1000 s, exposure bias: -2 step

focal length = 7mm, max aperture : 2.9685

no flash, auto white balance, no zoom, EXIF version 0220

279KB

(no camera information)

1920 x 1080 pixels, 24-bit, 96 dpi (vertical and horizontal)

focal length : 35mm

272KB

(no camera information) \

1920 x 1080 pixels, 24-bit, 96dpi (vertical and horizontal)

90.1KB

Canon PowerShot S2 IS,

1024 x 768 pixels, 24-bit, 72 dpi (vertical and horizontal)

compressed bits/pixel: 5

F-stop: f/4, exposure: 1/160 s, exposure bias: 0 step

focal length: 14mm, max aperture: 3.625

noflash, auto white balance

152KB

camera maker: OLYMPUS IMAGING CORP., model: FE310,X840,C530

1024 x 768 pixels, 314 dpi, 24-bit

f-stop : f/3.3, exposure: 1/30 s., ISO speeed: ISO – 180

exposure bias: 0-step, focal length: 6mm., max aperture: 2.97, metering mode: center weighted average, no flash

219 KB

Okay guys you might be confused at those details. let me explain them in a bit.

At the first lines, we show the manufacturer and the model of the camera used. We have canon and olympus. The next line shows the number of pixels or the size of the image itself. Then we have the dpi, or the dots per inch. This is the resolution of the camera. It basically shows how much dots does an inch contain. The higher the dpi, the higher the resolution of the camera, and also, the higher the image size on drive. 🙂 As a proof of that, let’s look at images 4 and 5 because they have the same size. Image 5 has dpi of 314 while image 4 has dpi of 72. We can see that image five is 219KB while image 4 is 152KB. Well, this may be inconsequential in small sized images, but in dealing with bigger images, quality versus image size is a big deal. It is oftentimes the question of how much resolution can I lose without really damaging the quality of the picture so that i can send it through e-mail?

Compressed bits per pixel refers to the number of bits that is used to describe a pixel. It tells how much information a pixel contains. F-stop is the aperture that controls the amount of light that enters the camera. It relates the focal length of the camera to the diameter of the aperture. For example, in image 5,  if the f-stop is f/3.3, it means that the diameter of the aperture is 6mm/3.3. Exposure is the amount of time that the camera is exposed to light. a higher exposure means that more light hits the photographic medium, and unless the camera is moved, or the objects move, or the camera is saturated, the image becomes clearer. Exposure bias is the correction the photographer places on the camera if the camera overexposes or underexposes. This is oftentimes for visual clarity and information.

The ISO speed another feature of a camera that controls the amount of light by controlling the sensitivity of the film or sensor. In cameras that uses films, the ISO speed of the camera is matched to that of the film. In digital cameras, the ISO speed is much more flexible, offering another control to the photographer to match the settings to that of the ambient light, surroundings, etc. Another way to control the sensitivity of the camera to the intensity or brightness of light is to control how the camera measures it. This is given by the metering mode.

The other properties of camera, such as the focal length, and the aperture are just properties of the lenses of the camera themselves.

For the next part of the activity, let me show you the difference of a binary, grayscale, indexed and true color image.

(A) True color (256 colors). (B) Binary. (C) Grayscale. (D) Indexed image, 2-colors. (E) Indexed Image, 4-colors. (F)Indexed image, 8-colors. (G) Indexed Image, 16 colors. (H) Indexed Image, 32 – colors. (I) Indexed Image, 64-colors. (J) Indexed image, 128-colors

The figure above shows a single image in 10 different types. We have the true color in 256 bit, black and white, grayscale and indexed images from 2-color to 128 color. In the hard-disk, the true color is 29 KB. The binary is considerably smaller in size, only about 21KB. The grayscale is 25KB. Now, it is worth noting that the indexed image is bigger than the true color image. (D-J is 30KB, 30KB, 32KB, 32KB, 31KB, 30KB, 29KB, respectively). We can see that indexing the image in 128 colors does not change the quality of the image, at least to a human observer. Though grayscale and binary has smaller file size, the smaller file size cannot compensate for the information lost. There are images in which the color is not important, but for this image, for the observer to appreciate the flower, full color, or at least indexing it at 128 color, is needed.

There are two types of image file format, classified according to how the images are formed. One is the raster images, which are composed of pixels and the vector images, which is composed of many tiny lines and curves called paths. [1] Let’s talk about them one by one. There are a lot of file extensions for the two types of images. I will only discuss the famous.

1. Vector images

Vector images are images that are created using paths, in contrast to raster images which are made up of a grid of pixels. Thus, the images can be called as wireframe type images. These type of images must be created using specific computer softwares, since each path in the image has its own properties such as node positions, node locations, line lengths and curves. Vector images are very mathematical in nature, as to create these paths. [1,2] Since these images are not pixelated, vector graphics do not lose any quality if scaled into a larger size. This makes it ideal for logos, whose scale should be flexible.

an example of a vector image

Vector file formats were the first kind of images that were used when the need to display output in devices came. The first display devices such as the CRT were similar to oscilloscopes, capable of producing and displaying geometrical shapes. When the need to store these images arose, the images were stored in a certain fashion. First, an image was subdivided into its simplest elements, meaning the paths. Then the image was produced, drawing each of its elements in the specified order. Lastly, data was exported as a list of drawing operations and the mathematical descriptions of the elements (size, shape, position) were written into the storage device in the order in which they are displayed. [3]

Some file types are shown below:

CGM (Computer Graphics Metafile)

• created by committees working under the International Standards Organization and the American Standards National Institute. It was designed as a common format for the platform independent interchange of bitmap and vector data, and used in conjunction with many different input and output devices. CGM sometimes incorporates extensions for bitmap images.[4]

• A very feature-rich format which attempts to provide the needs in many fields such as graphic arts, technical illustration, cartography, visualization, electronic publishing and others.

Gerber File Format

•  A standard electronics industry file format, often used in PCB manufacturing. The contents is in ASCII text. The contents are commands for a machine called photoplotter, which creates the picture on a photographic film by precise control of light.

There are other file types, often times extensions of files used by certain softwares such as the following:

AI (Adobe Illustrator), CDR(CorelDraw), HVIF(Haiku Vector Icon Format), ODG(OpenDocumentGraphics) and others.

2. Raster Images

Raster Images are images that are composed of tiny dots in a grid. All images I have displayed earlier (except for the example in vector) are raster images. The information of the picture are contained in each of the dots, and the information that is stored is only the color information. In contrast to vector images, no information about any line, angle or any mathematical shape is stored. Unlike vector images, the quality of raster images depend on the resolution; meaning the scaling is limited. If a raster image is scaled down, some pixel information have to be thrown away. and when a raster image is to be scaled up, to prevent loss of resolution, new pixels must be generated, of which the information it contains must depend on its neighboring pixels using a process called interpolation. There many techniques on resizing a raster image and compromising only a little bit of quality, but we will not delve on that here. 🙂

I will discuss some famous raster file extensions.

1. Bitmap (.BMP, .DIB)

• The bitmap as a raster file type image was created by microsoft and was first integrated into the Windows 3.0 os. This is due to the fact that BMP files were highly dependent on the graphics of the hardware used. The DIB supported only up to 16-bit of information per pixel then. (sorry i have no example. wordpress does not allow bmp. they’re not pro-microsoft, I guess. haha)

2. Joint Photographic Experts Group (.JPEG, JPG)

• JPEG is a method of lossy compression. It was a standard that was created by the group bearing the same initials in 1986, and since then have been adding more standards. The compression algorithm is a discrete cosine transform, converting the spatial information into frequency information then storing it. Since the transform is discrete, the resulting coefficients are quantized. In this compression scheme, the high frequency values are disregarded. This types of images are not for scientific use, nor for activities requiring high information. It is solely for human vision, since the omission of high frequency terms are not sensed by the eye. For examples, look at images in the web.

3. Graphics Interchange Format (GIF)

• GIF images employ a lossless compression format called the Lempel-Ziv-Welch lossless compression technique and was introduced to the world in 1987 by CompuServe. This was to provide a color format for file downloading areas of CompuServe. However, in 1995, the compression technique was patented by Unisys. This and the fact the GIF images are limited by the 256 color scheme made it undesirable. (http://en.wikipedia.org/wiki/Graphics_Interchange_Format)

4. Portable Network Graphics (PNG)

• The PNG is a lossless compression format that was desired as a replacement for the GIF. This is because the algorithm for the GIF was patented, and some limitations which rendered the GIF undesirable. Since the PNG employs a lossless compression format, it is often used in the scientific community.

Other Raster File Formats are the TIFF, IMG, DEEP, and others

The last part of the activity is to explore some SciLab syntax. Those are the following:

im = imread(‘imagefile’)// reads the image and name’s it as im

imshow(im)//shows image im

bw = im2bw(im, thresh)// converts im into a black and white image with respect to some threshold and then stores it as bw

histplot(numberofbins, array)// creates a histogram with number of bins.

imwrite(‘file’)// writes an image

imfinfo(‘file’, format)// returns information about the image file

 

The author would like to give himself a credit of 10/10. He would like to thank the ones who helped him: Hannah, and Abby. All of the images used are from the web.

sources:

fanpop.com
a1128.g.akamai.net
http://en.wikipedia.org/wiki/Dots_per_inch
http://www.dpreview.com/
http://www.laesieworks.com/digicom/compression.html
http://www.picturecorrect.com/tips/what-is-an-f-stop/

Using Exposure Bias To Improve Picture Detail

http://www.howstuffworks.com/what-is-iso-speed.htm

http://www.pcmag.com/article2/0,2817,1159326,00.asp
http://en.wikipedia.org/wiki/Graphics_Interchange_Format
1. Cousins, C. “Vector vs. Raster: What do I use?”. Design Shack. 6th Jun 2012. Accessed on 18 Jun 2013. Retrieved from http://designshack.net/articles/layouts/vector-vs-raster-what-do-i-use/
2. Faiza (username). “Basics, Difference Between Pixel and Vector-based Graphics”. Webdesigner. 13 Mar 2011. Accessed on 18 Jun 2013. Retrieved from http://www.1stwebdesigner.com/design/pixel-vector-graphics-difference/
3. Murray, James and vanRyper, Williams. Encyclopedia of File formats 2nd ed. Sebastopol: O’Reilly 1996. Print. Retrieved from http://netghost.narod.ru/gff/graphics/book/ch04_02.htm
4. Fileformat. “CGM File Format Summary”. Accessed on 18 Jun 2013. Retrieved from http://www.fileformat.info/format/cgm/egff.htm

 

Learning Scilab

In our Applied Physics 186 activity, we were told to tinker with Scilab programming language. It is a bit similar to Matlab, the language im familiar with. We used scilab to create some patterns and images, and yeah, it was fun.

For starters, we created a plot of a sine wave. The code was already given to us:

The code was pretty straightforward:

t = [0:0.05:100];
y = sin(t);
plot(t,y);

another code which was given to us was the code to create an image of a circular aperture. well, it was just a circle though, and to create it, some boolean was needed.

 

 

nx = 100; ny = 100; //defines the number of
elements along x and y
x = linspace(-1,1,nx); //defines the range
y = linspace(-1,1,ny);
[X,Y] = ndgrid(x,y); //creates two 2-D arrays of x
and y coordinates
r= sqrt(X.^2 + Y.^2); //note element-per-element
squaring of X and Y
A = zeros (nx,ny);
A (find(r<0.7) ) = 1;
f = scf();
grayplot(x,y,A);
f.color_map = graycolormap(32);

 

We were then instructed to create some patterns, as well as other shapes that we can create, as shown below (The codes are found in the last part of the post):

1. A centered square

2. Corrugated roof (sinusoid)

3. Grating along the x-direction:

4. Annulus

5. Circular aperture with graded transparency

I also created some other patterns:

A graded x_y grating:

An x grating with a beat frequency:

And an x-y grating with a beat frequency:

I also created other stuffs with the Fast Fourier transform, but that would have to wait. 🙂

I would like to thank Hannah Villanueva and Abby Jayin for the help of some of the codes. I would like to give myself a grade of 11/10 since I was able to create other patterns, aside from the patterns that were required.

codes:

centered square:

x = linspace(-1,1,100);
y = linspace(-1,1,100);
[X,Y] = ndgrid(x,y);
A = zeros(100,100);
A(find(abs(X)<0.7 & abs(Y)<0.7)) = 1;
f = scf();
grayplot(x,y,A);
f.color_map = graycolormap(32);

Corrugated roof:

x = linspace(-1,1,500);
y = linspace(-1,1,500);
[X,Y] = ndgrid(x,y);
x_sin = sin(2*%pi*X*10);
f = scf();
grayplot(x,y,x_sin);
f.color_map = graycolormap(32);

x-grating

x = linspace(-1,1,500);
y = linspace(-1,1,500);
[X,Y] = ndgrid(x,y);
x_sin = sin(2*%pi*X.*10);
A = zeros(500,500);
A(find(x_sin>0)) = 1;
f = scf();
grayplot(x,y,A);
f.color_map = graycolormap(32);

Annulus:

nx = 500; ny = 500;
x = linspace(-1,1,nx);
y = linspace(-1,1,ny);
[X,Y] = ndgrid(x,y);
r = sqrt(X.^2 + Y.^2);
A = zeros(nx,ny);
A_2 = zeros(nx,ny);
A(find(r<.7)) = 1;
A_2(find(r<0.3)) = 1;
ann = A – A_2;
f = scf();
grayplot(x,y,ann);
f.color_map = graycolormap(32);

Circular aperture with graded transparency:

nx = 500; ny = 500;
x = linspace(-1,1,nx);
y = linspace(-1,1,ny);
[X,Y] = ndgrid(x,y);
r = sqrt(X.^2 + Y.^2);
gauss = exp((-r.^2)/0.4)
A = zeros(nx,ny);
A(find(r<.7)) = 1;
gauss_circ = gauss.*A;
f = scf();
grayplot(x,y,gauss_circ);
f.color_map = graycolormap(32);

data reacquisition

What we did in class is that we scanned a hand-drawn plot from an old thesis[1], and try to recreate the plot by obtaining the pixel values. The aim of the activity is to be able to recreate the plot.

The image was scanned, and then opened in paint. Using the tick marks that can be found in the image, I obtained an equation that relates the pixel values to the real-world data from which the graph stemmed from. The x and the y axis had different relation equation given by the following:

f(x) = 5.02E-5*x + 1.15E-5

f(y) = 1.43E-5*y -6.10E-5

where f(x) and f(y) are the real world numbers and x and y are the distances from the origin of the graph in pixels. The y coordinate of the pixel posed a little problem since the values for y pixels go downward. The remedy is just to subtract the current pixel value from the value of the origin to find the distance in pixels.

Points along the curvature of the plot are then tabulated. Many plot points are obtained so that the resulting graph would be much more accurate to the real graph. I did both of the curves, the dashed and the continuous one, as seen from the image below.

The yellow and red dots are the graph that i obtained after getting the pixel values and converting them into real world values. It can be observed that some discrepancy exists. this is due to the fact that the scanned image is slightly tilted. I have not put a correcting factor on this because there is not enough time left.

I would like to give myself 11 total points, since I was able to overlay the graph that i obtained to the original one.

[1] Domingo, Zenaida (1980) Computer simulation of the focusing properties of selected solar concentrations, M.S. Thesis. UP Dilimanb